Второй постулат динамики записывают несколькими способами, например, используя импульс. Указанная формулировка встречается гораздо реже обычного, однако решает ряд задач школьной, университетской механики.
Второй закон Ньютона в импульсной форме
В общем случае запись главного постулата динамики включает три составляющие:
- массу, m;
- ускорение, a;
- воздействие, F.
Второй закон Ньютона в импульсной форме записывают, определив изначально импульс тела
Измеряется результатом деления произведения килограмма, метра на секунду –
Очевидно: описываемая мера механического движения — величина векторная, совпадающая с направлением
Физика использует понятие импульса силы
Измеряется произведением ньютона, секунды –
Импульс действующей силы равен изменению импульса объекта.
Похожая формулировка:
Изменение импульса во времени равно величине действующей силы.
Второй закон ньютона в импульсной форме формула
Самостоятельно выразим требующуюся формулу, используя известную запись:
Определение ускорение гласит: данная величина характеризует увеличение, уменьшение скорости:
Аналогично:
– приобретённая, начальная скорости,
– изменение времени.
Зная стандартный вид постулата, выразим ускорение, приравняем к полученному выражению:
Части уравнения умножим на , получим:
Правая часть уравнения равна , преобразуем равенство, получим:
Глядя на получившуюся формулу сформулируем второй закон Ньютона через импульс.
Изменение импульса тела равно импульсу действовавшей на тело силы.
Формулировка аксиомы ньютоновской динамики, использующая понятие импульса, полностью соответствует виду, изначально выведенному учёным. Получить подобную запись возможно, учитывая оператор, называемый дифференциалом. Дифференциал функции d – приращение, изменение.
Формула a записывается видом:
Читается: «изменение скорости при изменяющемся времени».
Приравнивая правые части, получаем:
Умножаем части уравнения на m, сразу вносим массу под знак дифференциала:
Результат:
В каких случаях применяют импульсную форму
Некоторые задачи невозможно решить, применяя обычную формулу постулата динамики. Например, задания движения тела изменяющегося веса.
Русский механик, учёный Иван Всеволод Мещерский на основе импульсной формы вывел уравнение, позволяющее решать задачи перемещения объектов переменной массы. Уравнением Мещерского удобно выводить формулу Константина Эдуардовича Циолковского, использующуюся при проектировании баллистических, космических ракет. Указанные летательные аппараты — реальный пример тел, изменяющих вес.
Более приземлённые, обыденные задачи применения описываемой записи 2 постулата – движение двух сталкивающихся шаров, движение одного шара, ударяющегося о препятствие.
Пример использования
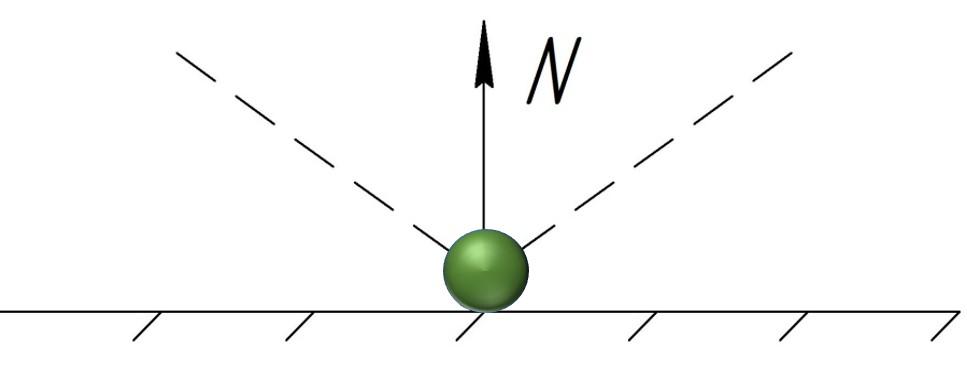
Пусть шарик, обладающий массой m, неизменяющейся скоростью , ударяется о стену под углом
, спустя
отлетает.
Принимаем допущение: стена гладкая, трение отсутствует. Шарик, ударяясь, испытывает воздействие силы упругости N.
Известно:
Сила, действующая на тело, является единственной, видоизменим запись:
Найдём , используя правило сложения векторов – векторный треугольник.
Потери скорости отсутствуют, вес остаётся прежним, следовательно, . Получившийся векторный треугольник равнобедренный. Неизвестный вектор:
N равна:
Второй закон Ньютона в импульсной форме позволяет решать задачи разного уровня значимости: школьные типовые задания, проекты космического масштаба.