В «Математических началах натуральной философии» Ньютона сформулирован закон, который в двадцатом веке охарактеризован Эйнштейном как главный постулат механики и считается фундаментом теоретической физики.
Второй закон Ньютона формулировка
Ньютон, формулируя постулат, связывал движущую силу и изменение количества движения.
Современная трактовка использует более привычные для восприятия термины, сегодня 2-й закон Ньютона звучит как:
В системах отсчёта, называемых инерциальными, материальная точка приобретает ускорение, сонаправленное силе или равнодействующей сил, являющихся возбудителями движения, и находящееся в прямо пропорциональной зависимости от неё. Также упомянутое ускорение обратно пропорционально массе движущейся материальной точки.
Трактовать постулат динамики можно через импульс – меру движения тела, численно равную результату умножения массы на скорость:
где p, m, v – импульс, масса, скорость тела или точки.
Вторая формулировка второго закона Ньютона гласит:
В системах отсчёта, называемых инерциальными, скорость изменения импульса, имеющего также название «количество движения», численно равно силе или равнодействующей сил, являющихся возбудителями движения материальной точки.
Область применения
2-й закон Ньютона применяют к материальным точкам – объектам массой, сосредоточенной в точке, и размерами, которыми допустимо пренебречь. Логичен вывод, что постулат механики работает в случаях, где масса тела остаётся постоянной. Также формулу свободно применяют в задачах движения центра масс системы, используя одноимённую теорему.
Формулировки отмечают ограниченность применимости закона инерциальными системами отсчёта. Однако, если внести силы инерции в равнодействующую, уравнение движения, составленное на основе постулата Ньютона, допустимо использовать в неинерциальных системах.
Вывод закона на основании проведённых опытов
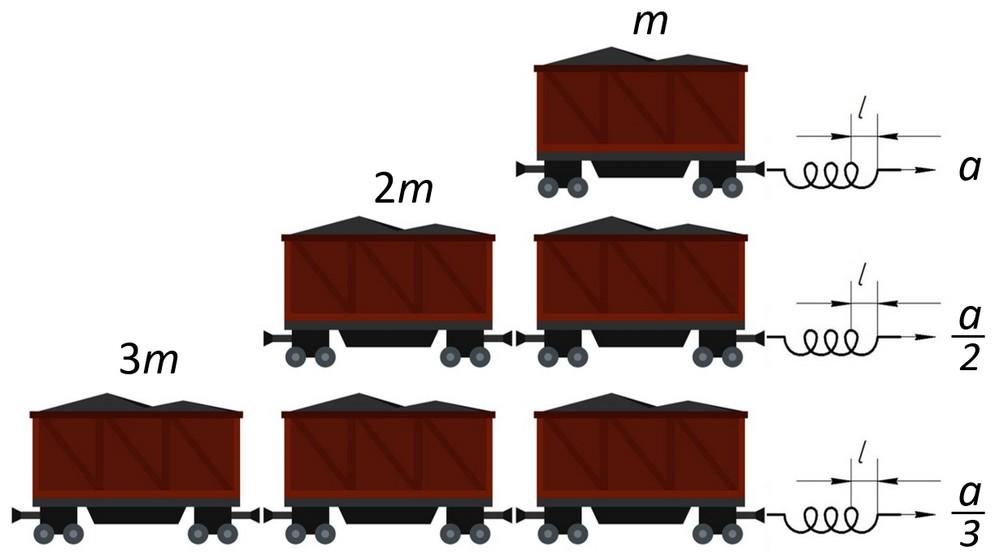
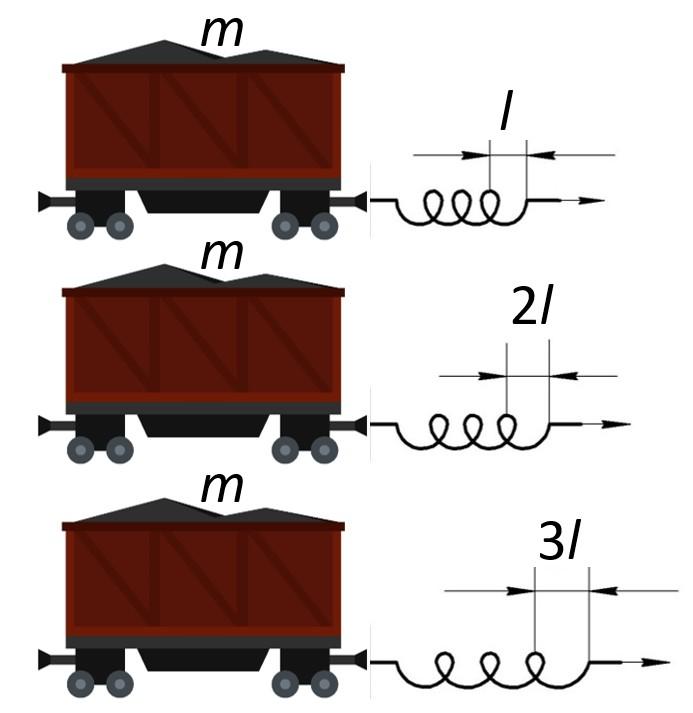
Изучаемый фундамент динамики (динамика – наука, изучающая движение) не удастся вывести путём математических вычислений, формулу доказывают опытом, представленным рисунком.
Тележка массой m взаимодействует с пружиной, растянутой на длину l. Если тянуть конец пружины, соблюдая выбранное значение деформации, тележка покатится по направлению воздействия, обладая ускорением a. Увеличим вес, добавив тележку, идентичную используемой, и снова потянем свободный конец пружины, следя за постоянностью удлинения. Зафиксируем уменьшение ускорения. Для полноты эксперимента, добавив третью тележку, повторим опыт и заметим, что значение ускорения меньше.
В эксперименте прикладываемая нагрузка оставалась неизменной, что контролировалось путём использования одной пружины, деформированной на величину l.
Рассмотрим произведение массы на ускорение тележки:
- для первого опыта:
;
- для второго:
;
- для третьего:
.
То есть, рассмотренное произведение одинаково и зависит от меры оказанного воздействия :
,
Вывод формулы второго закона Ньютона — видео.
Зависимость между массой и ускорением
Согласно проиллюстрированному опыту, ускорение объекта уменьшается настолько, насколько увеличивается масса. Результаты эксперимента для наглядности приведём в табличный вид:
[table id=2 /]
Вывод: ускорение обратно пропорционально массе.
Зависимость между силой и ускорением
Для отражения связи между ускорением и силой придадим продемонстрированному опыту другую форму. К тележке массой m приложим силу, увеличивающуюся по модулю. Изменение нагрузки фиксируется за счёт возрастающей деформации пружины, тянущей тележку. В качестве эталонного проведём знакомый эксперимент: будем тянуть тележку массой m при помощи пружины с удлинением l и зафиксируем ускорение системы, равное a. Далее воздействуем на объект в два раза сильнее, растянув пружину до значения деформации 2l, и заметим, увеличение ускорения тележки до 2a. Для закрепления результата снова увеличим усилие, под действием которого растягивается пружина. По закону Гука, деформация пружины напрямую зависит от меры воздействия. Увеличив значение удлинения до 3l, увидим, что тележка двинется с ускорением 3a.
Анализируя эксперимент, делаем вывод: ускорение прямо пропорционально действующей силе.
Единица измерения силы
Международная система единиц, в привычном обозначении СИ – система интернациональная, называет ньютоны в качестве единиц, в которых измеряется сила. Ньютоны – производные единицы, выраженные основными (к ним относится семь наименований) путём умножения или деления последних друг на друга:

Справка: Фамилия Ньютон пишется с заглавной буквы, одноимённое название единиц измерений записывается со строчной.
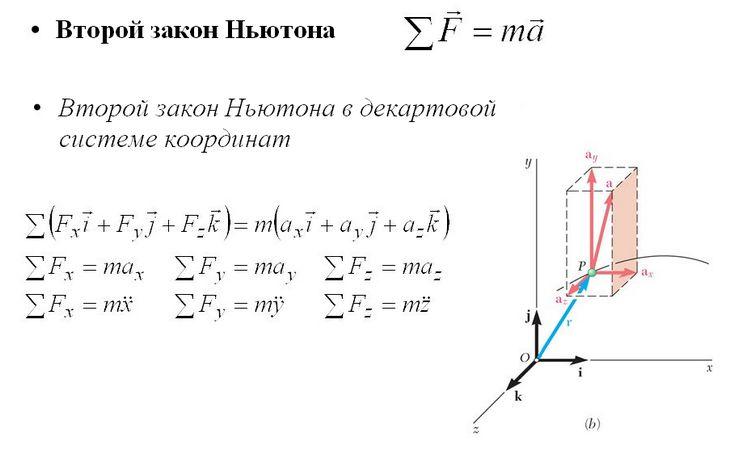
Формула второго закона Ньютона
Формулу, выражающую закон Ньютона, записывают различными формами, в зависимости от системы координат. Стандартная запись:
в декартовой прямоугольной системе координат выглядит следующим образом:

где ,
– орты или единичные векторы.
В сферической и цилиндрической системах запись усложнена, однако все виды формулы выражают одну взаимосвязь силы, ускорения и массы.
Равнодействующая сила
Интуитивно значение силы, действующей на тело, ясно, однако второй закон Ньютона определении вносит незнакомый термин – «равнодействующая», и изначально сложно уверенно утверждать, о каком воздействии говорится.
Мало кто способен назваться гением по физике, однако каждому понятно, что любое тело испытывает воздействие нескольких сил одновременно. Сюда относятся, например, силы тяжести, сопротивления воздуха или упругости, реакция опоры. Для удобства расчётов прикладываемые к объекту воздействия сформировывают в одно – равнодействующую.
Совместное действие находят суммированием векторов внешних сил, приложенных к телу:

На практике подобное осуществляется проецированием векторов на координатные оси:
Если присутствует воздействие пары сил, действующих вдоль одной прямой, равнодействующая определяется как:
– силы сонаправлены;
– воздействия противонаправлены (
)
Таким образом, больше не возникнет вопроса, как читается выражение , и изученный закон сразу будет формулироваться в мыслях.

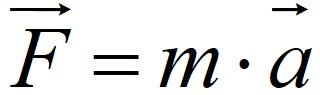
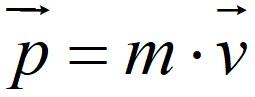





при изучении второго закона Ньютона всегда говорится о силе действия, но никогда не упоминается сила противодействия. неужели сила действия возникает в одиночку, а потому не имеет отношения к третьему закону Ньютона?